ÀNGULOS, TRIÁNGULOS Y
RELACIONES MÉTRICAS
Un ángulo es la parte del plano comprendida entre dos
semirrectas que tienen el mismo punto de origen o vértice.1 Suelen
medirse en unidades tales como el radián, el grado sexagesimal o el grado
centesimal.
Pueden estar
definidos sobre superficies planas (trigonometría plana) o curvas
(trigonometría esférica). Se denomina ángulo diedro al espacio comprendido
entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que
abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.
Un triángulo, en geometría, es un polígono
determinado por tres rectas que se cortan dos a dos en tres puntos (que no se
encuentran alineados, es decir: no colineales). Los puntos de intersección de
las rectas son los vértices y los segmentos de recta determinados son los lados
del triángulo. Dos lados contiguos forman uno de los ángulos interiores del
triángulo.
Por lo
tanto, un triángulo tiene 3 ángulos interiores, 3 ángulos exteriores, 3 lados y
3 vértices.
Si está
contenido en una superficie plana se denomina triángulo, o trígono, un nombre
menos común para este tipo de polígonos. Si está contenido en una superficie
esférica se denomina triángulo esférico. Representado, en cartografía, sobre la
superficie terrestre, se llama triángulo geodésico.
Las relaciones métricas en el triángulo son aquellas
tratan las relaciones entre longitudes o ángulos, entre las cuales se destaca
el Teorema de Pitágoras que es válido exclusivamente en el triángulo rectángulo
y se aplica sobre las dimensiones de los catetos, hipotenusa, la altura
relativa a la hipotenusa y los segmentos determinados sobre ésta como
proyecciones de los catetos de triángulo.
Clasificación de ángulos según su medida
| Agudo < 90° |
Recto = 90° |
Obtuso>90° |
 |
 |
 |
| Convexo < 180° |
Llano = 180° |
Cóncavo > 180° |
|
 |
 |
| Nulo = 0º |
Completo = 360° |
|
 |
 |
|
| Negativo < 0º |
Mayor de 360° |
|
 |
 |
|
Tipos de ángulos según su posición
Ángulos consecutivos
Ángulos consecutivos son aquellos que tienen el vértice y un lado común.
Ángulos adyacentes
Ángulos adyacentes son aquellos que tienen el vértice y un lado común, y los otros lados situados uno en polongación del otro.
Forman un ángulo llano.
Ángulos opuestos por el vértice
Son los que teniendo el vértice común, los lados de uno son prolongación de los lados del otro.
Los ángulos 1 y 3 son iguales.
Los ángulos 2 y 4 son iguales.
Clases de ángulos según su suma
Ángulos complementarios
Dos ángulos son complementarios si suman 90°.
Ángulos suplementarios
Dos ángulos son suplementarios si suman 180°.
Ángulos entre paralelas y una recta transversal
Ángulos correspondientes
Los ángulos 1 y 2 son iguales.
Ángulos alternos internos
Los ángulos 2 y 3 son iguales.
Ángulos alternos externos
Los ángulos 1 y 4 son iguales.
Ángulos complementarios o suplementarios
Dos ángulos son complementarios si la suma de sus ángulos es igual a 90o.
Si conocemos un ángulo, su ángulo complementario se puede encontrar restando la medida del mismo a 90o.
Ejemplo: ¿Cuál es el ángulo complementario de 43o?
Solución: 90o - 43o = 47o
Dos ángulos son suplementarios si la suma de sus grados es igual a 180o.
Si conocemos un ángulo, su ángulo suplementario se puede averiguar restando la medida del mismo a 180o.
Ejemplo: ¿Cuál es el ángulo suplementario de 143o?
Solución: 180o - 143o = 37o
TRIANGULOS
Clasificación de triángulos
Según sus lados
Triángulo equilátero
Tres lados iguales.
Triángulo isósceles
Dos lados iguales.
Triángulo escaleno
Tres lados desiguales
Según sus ángulos
Triángulo acutángulo
Tres ángulos agudos
Triángulo rectángulo
Un ángulo recto
El lado mayor es la hipotenusa.
Los lados menores son los catetos.
Triángulo obtusángulo
Un ángulo obtuso.
Segun sus angulos
- Triángulo rectángulo: si tiene un ángulo interior recto (90°). A los dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.
- Triángulo oblicuángulo: cuando ninguno de sus ángulos
interiores son rectos (90°). Por ello, los triángulos obtusángulos y
acutángulos son oblicuángulos.
- Triángulo obtusángulo: si uno de sus ángulos interiores es obtuso (mayor de 90°); los otros dos son agudos (menores de 90°).
- Triángulo acutángulo: cuando sus tres ángulos interiores son menores de 90°. El triángulo equilátero es un caso particular de triángulo acutángulo.
 |
 |
 |
| Rectángulo |
Obtusángulo |
Acutángulo |
|
 |
|
Oblicuángulos | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
CONGRUENCIA DE TRIANGULOS
Las condiciones mínimas que deben cumplir dos triángulos para que
sean congruentes se denominan criterios de congruencia, los cuales son:
- Criterio LLL: Si en dos triángulos los tres lados de uno son
respectivamente congruentes con los del otro, entonces los triángulos
son congruentes.
- Criterio LAL: Dos lados y un ángulo compredido entre ellos.
- Criterio ALA: Si dos ángulos y el lado entre ellos son
respectivamente congruentes con los mismos de otro triángulo, entonces
los triángulos son congruentes.
- Criterio LLA: Dos triángulos son congruentes si tienen respectivamente iguales dos lados y el ángulo opuesto al mayor de ellos.
Postulado LAL
LAL significa lado-ángulo-lado.
Dos triángulos son congruentes si tienen dos lados y el ángulo determinado por ellos respectivamente iguales.
Postulado ALA
ALA significa ángulo-lado-ángulo.
Dos triángulos son congruentes si tienen dos ángulos y el lado común a ellos, respectivamente, iguales.
Postulado LLA
LLA significa lado-lado-ángulo
Dos triángulos son congruentes si tienen respectivamente iguales dos lados y el ángulo opuesto al mayor de ellos.
Postulado LLL
LLL significa lado-lado-lado.
Dos triángulos son congruentes si tienen sus tres lados respectivamente iguales.
PROBLEMAS DE SEMEJANZA DE TRIANGULOS
1Dos triángulos son semejantes si tienen dos ángulos iguales.
2 Dos triángulos son semejantes si tienen los lados proporcionales.
3 Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.
Semejanza de triángulos rectángulos
1Dos triángulos rectángulos son semejantes si tienen un ángulo agudo igual.
2Dos triángulos rectángulos son semejantes si tienen los dos catetos proporcionales.
3Dos triángulos rectángulos son semejantes si tienen proporcionales la hipotenusa y un cateto.
Ejemplos prácticos
1. Determinar
la altura de un edificio que proyecta una sombra de 6.5 m a la misma
hora que un poste de 4.5 m de altura da una sombra de 0.90 m.
2.Los
catetos de un triángulo rectángulo que miden 24 m y 10 m. ¿Cuánto
medirán los catetos de un triángulo semejante al primero cuya hipotenusa
mide 52 m?
TEOREMA DE TALES
Cuando en geometría hablemos del Teorema de Tales (o Thales), debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.
El primero de ellos se refiere a la construcción de un triángulo que sea semejante a otro existente (triángulos semejantes son los que tienen iguales ángulos).
Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos (los circuncentros se encuentran en el punto medio de su hipotenusa).
Primer teorema
Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes
si tienen los ángulos correspondientes iguales y sus lados son
proporcionales entre si. El primer teorema de Tales recoge uno de los
postulados más básicos de la geometría, a saber, que:
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.
Entonces, veamos el primer Teorema de Tales en un triángulo:
 |
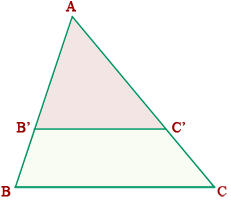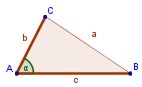
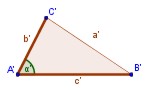
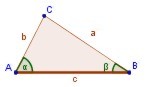
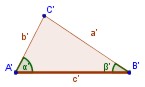
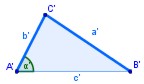
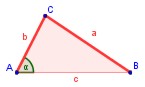
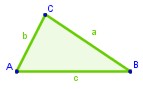
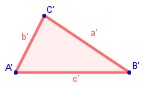
Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.
Lo que se traduce en la fórmula
|
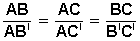
Ver: PSU: Geometría;
Hagamos un ejercicio como ejemplo:
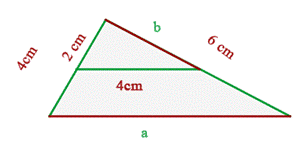
En el triágulo de la derecha, hallar las medidas de los segmentos a y b.
Apicamos la fórmula, y tenemos
|
 |
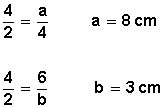
Como vemos, la principal aplicación del teorema, y la razón de su fama,
se deriva del establecimiento de la condición de semejanza de
triángulos, a raíz de la cual se obtiene el siguiente corolario.
Corolario
Al establecer la existencia de una relación de semejanza entre ambos
triángulos se deduce la necesaria proporcionalidad entre sus lados.
Ello significa que la razón entre la longitud de dos de ellos en un
triángulo se mantiene constante en el otro.
 |
| Una aplicación del Teorema de Tales. |
Por ejemplo, en la figura de la izquierda se observan dos triángulos
que, en virtud del Teorema de Tales, son semejantes. Entonces, como
corolario, el cociente entre los lados A y B del triángulo pequeño es
el mismo que el cociente entre los lados D y C en el triángulo grande.
En virtud del teorema de Tales, ambos triángulos son semejantes y se cumple que:
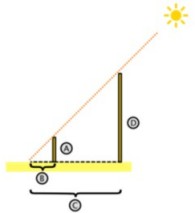
Este corolario es la base de la geometría descriptiva. Su utilidad es evidente; según Heródoto, el propio Tales empleó el corolario de su teorema para medir la altura de la pirámide de Keops en Egipto.
La leyenda de Tales y las pirámides
Según la leyenda (relatada por Plutarco), Tales de Mileto en un viaje a Egipto, visitó las pirámides de Guiza (Keops, Kefrén y Micerinos), construidas varios siglos antes.
Admirado ante tan portentosos monumentos, quiso saber su altura.
La leyenda dice que solucionó el problema aprovechando la semejanza de triángulos (y bajo la suposición de que los rayos solares incidentes eran paralelos).
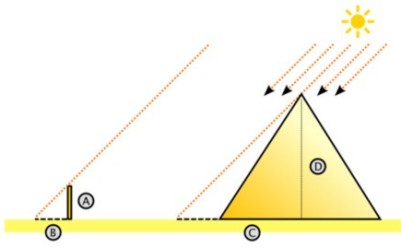
Así, estableció una relación de semejanza (Primer teorema de Tales)
entre dos triángulos rectángulos, los que se grafican en la figura a la
derecha.
Por un lado el que tiene por catetos (C y D) a la longitud de la sombra de la pirámide (C, conocible) y la longitud de su altura (D, desconocida), y por otro lado, valiéndose de una vara (clavada en el suelo de modo perfectamente vertical) otro cuyos catetos conocibles (A y B) son, la longitud de la vara (A) y la longitud de su sombra (B). Como en triángulos semejantes, se cumple que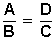 
, por lo tanto la altura de la pirámide es 
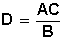, con lo cual resolvió el problema.
Otra variante del Teorema de Tales
 |
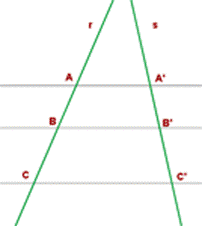Del primer teorema de Tales se deduce además lo siguiente
(realmente es otra variante de dicho teorema, y, a su vez, consecuencia
del mismo):
Si dos rectas cualesquieras (r y s) se cortan por varias rectas
paralelas (AA’, BB’, CC’) los segmentos determinados en una de las
rectas (AB, BC) son proporcionales a los segmentos correspondientes en
la otra (A’B’, B’C’).
|
Ejercicios
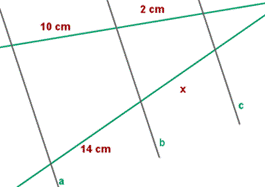
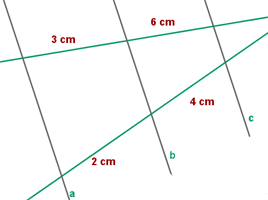
1. Las rectas a, b y c son paralelas. Hallar la longitud de x.
2.Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?
Sí, porque se cumple el teorema de Thales.
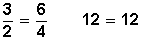
Una aplicación inmediata de este teorema sería la división de un
segmento en partes iguales, o en partes proporcionales a números dados
Aplicación del Primer Teorema de Tales
Una aplicación del teorema de Tales se utiliza para dividir un segmento en varias partes iguales (con ayuda de compás, regla y escuadra o cartabón).
Ejemplo
Dividir el segmento AB en 3 partes iguales
 |
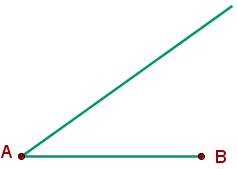1. Se dibuja una semirrecta de origen el extremo A del segmento. |
 |
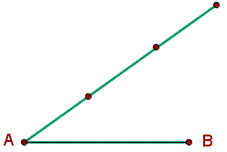2. Tomando como unidad cualquier medida, se señalan en la semirrecta 3 unidades de medida a partir de A. |
 |
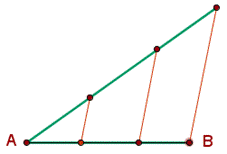3. Por cada una de las divisiones de la semirrecta se trazan rectas
paralelas al segmento que une B con la última división sobre la
semirrecta. Los puntos obtenidos en el segmento AB determinan las 3
partes iguales en que se divide. |
Segundo teorema
El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:
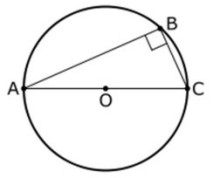
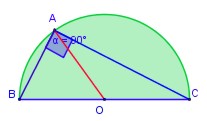
Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el ángulo ABC, es recto.
Este teorema (véase figuras 1 y 2), es un caso particular de una propiedad de los puntos cocíclicos y de la aplicación de los ángulos inscritos dentro de una circunferencia.
 |
 |
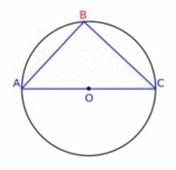Figura 1.
Ilustración del enunciado del segundo teorema de Tales de Mileto. |
Figura 2.
Siempre que AC sea un diámetro, el ángulo B será constante y recto. |
Demostración:
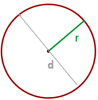
En la circunferencia de centro O y radio r (véase figura 3), los segmentos
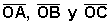
son iguales por ser todos radios de la misma circunferencia.
Por lo tanto, los triángulos AOB y BOC son isósceles.
La suma de los ángulos del triángulo ABC es:
2α + 2β = π (radianes) (180º)
Dividiendo ambos miembros de la ecuación anterior por dos, se obtiene:
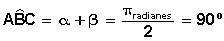
Con la expresión anterior el segundo teorema queda demostrado. |
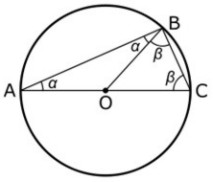
Figura 3.
Los triángulos AOB y BOC son isósceles. |
Semicircunferencia
Como la condición para este enunciado es que la hipotenusa
corresponda al diámetro de una circunferencia, también se puede expresar
como que el triángulo está inscrito en una semicircunferencia.
Entonces, el Teorema de Tales dirá que "todo triángulo inscrito en una semicircunferencia es rectángulo con hipotenusa igual al diámetro".
Demostración
Sea el triángulo BCA (en la figura superior)
Como OA y OB son iguales (radios de la semicircunferencia) , los ángulos ABO y BOA también son iguales y como OA y OC también son iguales, los ángulos OAC y OCA son iguales. Por tanto, ángulo BAC es igual a la suma de ABC y ACB.
Teniendo en cuenta que la suma de los tres ángulos interiores de un triángulo es 180º, el ángulo BAC debe ser recto.
Corolarios
Corolario 1
“En todo triángulo rectángulo la longitud de la mediana correspondiente a la hipotenusa es siempre la mitad de la hipotenusa.”
|
Ya que aplicando el teorema anterior, se sabe que para cualquier posición que adopte el vértice B vale la igualdad, OA = OB = OC = r, donde OB es la mediana de la hipotenusa, (véase figura 3).
Corolario 2
“La circunferencia circunscripta a todo triángulo rectángulo
siempre tiene radio igual a la mitad de la hipotenusa y su
circuncentro se ubicará en el punto medio de la misma.”
|
El corolario 2 también surge de aplicar el teorema anterior, para una comprensión intuitiva basta observar la figura 2.
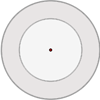
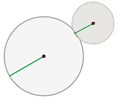
Aplicación del Segundo Teorema de Tales
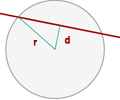
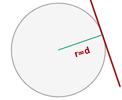
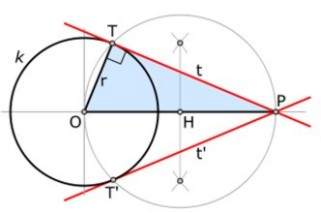
Construcción de tangentes (líneas rojas en la figura a la derecha) a una circunferencia k desde un punto P, utilizando el segundo teorema de Tales.
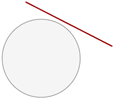
Este segundo teorema (de Tales de Mileto) puede ser aplicado para trazar las tangentes a una circunferencia k dada, que además pasen por un punto P conocido y externo a la misma (véase figura ).
Se supondrá que una tangente cualquiera t (por ahora desconocida) toca a la circunferencia k en un punto T (también desconocido por ahora).
Se sabe por simetría que cualquier radio r de la circunferencia k es perpendicular a la tangente del punto T que dicho radio define en la misma, por lo que concluimos que ángulo OTP es necesariamente recto.
Lo anterior implica que el triángulo OTP es rectángulo.
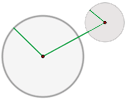
Recordando el corolario 2 del segundo teorema de Tales podemos deducir que entonces el triángulo OTP es inscribible en una circunferencia de radio mitad de la hipotenusa OP del mismo.
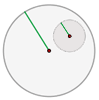
Entonces, marcando el punto H como punto medio de la hipotenusa OP y haciendo centro en el mismo, podemos dibujar una segunda circunferencia auxiliar (gris en la figura) que será la que circunscribe al triángulo OTP.
Esta última circunferencia trazada interceptará a la circunferencia k en dos puntos T y T', estos son justamente los puntos de tangencia de las dos rectas que son simultáneamente tangentes a k y además pasan por el punto P, ahora ya conocidos los puntos T y T' solo basta trazar las rectas TP y T'P (rojas en la figura) para tener resuelto el problema.
i dos rectas cualesquieras se cortan
por varias rectas paralelas, los segmentos determinados en una de las
rectas son proporcionales a los segmentos correspondientes en la otra.
Ejercicios
1.Las rectas a, b y c son paralelas. Halla la longitud de x.
2.Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?
Sí, porque se cumple el teorema de Thales.
El teorema de Thales en un triángulo
Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.
Hallar las medidas de los segmentos a y b.
Aplicaciones del teorema de Thales
El teorema de Thales se utiliza para dividir un segmento en varias partes iguales.
Ejemplo
Dividir el segmento AB en 3 partes iguales
1. Se dibuja una semirrecta de origen el extremo A del segmento.
2. Tomando como unidad cualquier medida, se señalan en la semirrecta 3 unidades de medida a partir de A.
3. Por
cada una de las divisiones de la semirrecta se trazan rectas paralelas
al segmento que une B con la última división sobre la semirrecta. Los
puntos obtenidos en el segmento AB determinan las 3 partes iguales en
que se divide.
TEOREMA DE PITAGORAS
El
teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa ("el lado de mayor longitud del triángulo rectángulo") es igual a la suma de los cuadrados de los catetos (
los dos lados menores del triángulo, los que conforman el ángulo recto).
Teorema de Pitágoras
En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Pitágoras de Samos
|
cuando se va a hallar la hipotenusa se Suma. ejemplo: h^2= a^2 + b^2
cuando se va a hallar un cateto se Resta. ejemplo: c^2= a^2 - h^2
De la ecuación (
1) se deducen fácilmente 3 corolarios de aplicación práctica:
1
La hipotenusa de un triángulo rectángulo mide 405.6 m y la proyección de un cateto sobre ella 60 m. Calcular:
1 Los catetos.
2 La altura relativa a la hipotenusa.
3 El área del triángulo.
2
Calcular los lados de un triángulo rectángulo sabiendo que la
proyección de uno de los catetos sobre la hipotenusa es 6 cm y la altura
relativa de la misma
cm.
3
Una escalera de 10 m de longitud está apoyada sobre la pared. El
pie de la escalera dista 6 m de la pared. ¿Qué altura alcanza la
escalera sobre la pared?
4
Determinar el lado de un triángulo equilátero cuyo perímetro es
igual al de un cuadrado de 12 cm de lado. ¿Serán iguales sus áreas?
5Calcular el área de un triángulo equilátero inscrito en una circunferencia de radio 6 cm.
6
Determinar el área del cuadrado inscrito en una circunferencia de longitud 18.84 cm.
7
En un cuadrado de 2 m de lado se inscribe un círculo y en este
círculo un cuadrado y en este otro círculo. Hallar el área comprendida
entre el último cuadrado y el último círculo.
8
El perímetro de un trapecio isósceles es de 110 m, las bases miden 40 y 30 m respectivamente. Calcular los lados no paralelos y el área.
9
A un hexágono
regular 4 cm de lado se le inscribe una circunferencia y se le
circunscribe otra. Hallar el área de la corona circular así formada.
10 En una circunferencia una cuerda mide 48 cm y dista 7 cm del centro. Calcular el área del círculo.
11
Los catetos de un triángulo inscrito en una circunferencia miden 22.2
cm y 29.6 cm respectivamente. Calcular la longitud de la circunferencia y
el área del círculo.
12Sobre un círculo de 4 cm de radio se traza un ángulo central de 60°. Hallar el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente.
Calcular los lados de un triángulo rectángulo
sabiendo que la proyección de uno de los catetos sobre la hipotenusa es 6
cm y la altura relativa de la misma
cm.
·
Una escalera de 10 m de longitud está apoyada
sobre la pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura
alcanza la escalera sobre la pared?
Determinar el lado de un triángulo equilátero
cuyo perímetro es igual al de un cuadrado de 12 cm de lado. ¿Serán
iguales sus áreas?
Pcuadrado = 12 · 4 = 48 cm
Ptriángulo = 48 cml = 48 : 3 = 16 cm
A = 122 = 144 m²
|
Calcular el área de un triángulo equilátero inscrito en una circunferencia de radio 6 cm.
El centro de la circunferencia es el baricentro. Por tanto:
PROPIEDADES DE LOS POLIGONOS
Polígono
En geometría, un polígono es una figura plana compuesta por una secuencia finita de segmentos rectos
consecutivos que cierran una región en el espacio. Estos segmentos son
llamados lados, y los puntos en que se intersectan se llaman vértices.
El interior del polígono es llamado a veces su cuerpo. El polígono es el
caso bidimensional del politopo,
figura geométrica general definida para cualquier número de
dimensiones. A su vez, un politopo de tres dimensiones se denomina poliedro, y de cuatro dimensiones se llama polícoro.
La palabra polígono deriva del griego antiguo πολύγωνος ( polúgonos), a su vez formado por πολύ ( polú) ‘muchos’ y γωνία ( gōnía) ‘ángulo’. 1 2 3 Aunque hoy en día los polígonos son usualmente entendidos por el número de sus lados.
La noción geométrica elemental ha sido adaptada de distintas maneras
para servir a propósitos específicos. Los matemáticos a menudo les
interesa solo la línea poligonal cerrada y los polígonos simples, los
cuales no se intersecan por sí mismos, y pueden definir un polígono de
acuerdo a ello. Es requisito geométrico que dos lados que se intersecan
en un vértice formen un ángulo no llano (distinto a 180º), ya que de
otra manera los segmentos se considerarían partes de un lado único, sin
embargo, matemáticamente, esos vértices podrían permitirse algunas
veces. En el ámbito de la computación, la definición de polígono ha sido
ligeramente alterada debido a la manera en que las figuras son
almacenadas y manipuladas en la computación gráfica para la generación de imágenes.
Ángulo central de un polígono regular
Es el formado por dos radios consecutivos.
Si n es el número de lados de un polígono:
Ángulo central = 360° : n
Ángulo central del pentágono regular= 360° : 5 = 72º
Ángulo central de una circunferencia
El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.
ANGULO INTERIOR DE UN POLIGONO
En geometría, un ángulo interior o ángulo interno es un ángulo formado por dos lados de un polígono que compartiendo un extremo común, está contenido dentro del polígono. Un polígono simple tiene sólo un ángulo interno por cada vértice y está situado del lado opuesto del polígono.
Si todos los ángulos interiores de un polígono no superan los 180 grados sexagesimales o  radianes, se clasifican como polígonos convexos. Si existe por lo menos un ángulo superior a 180 grados o radianes, se trata de un polígono cóncavo.
Si todos los ángulos interiores de un polígono convexo son iguales y todos sus lados tienen la misma longitud, se trata de un polígono regular. En caso contrario, se trata de un polígono irregular.
PERIMETRO Y AREA DE POLIGONO REGULARES
 
| A | | | | | | | | | | | | | | | | | | | | | | | | | | | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
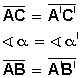
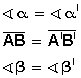
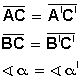
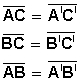
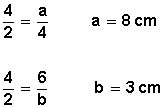
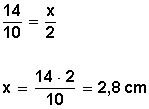
